LIS
부분수열을 먼저 이해하자. 수열의 부분 수열이란 수의 순서는 유지한 채 몇 개의 수를 제거해서 얻을 수 있는 수열을 의미한다.

가장 긴 증가하는 부분 수열(LIS)
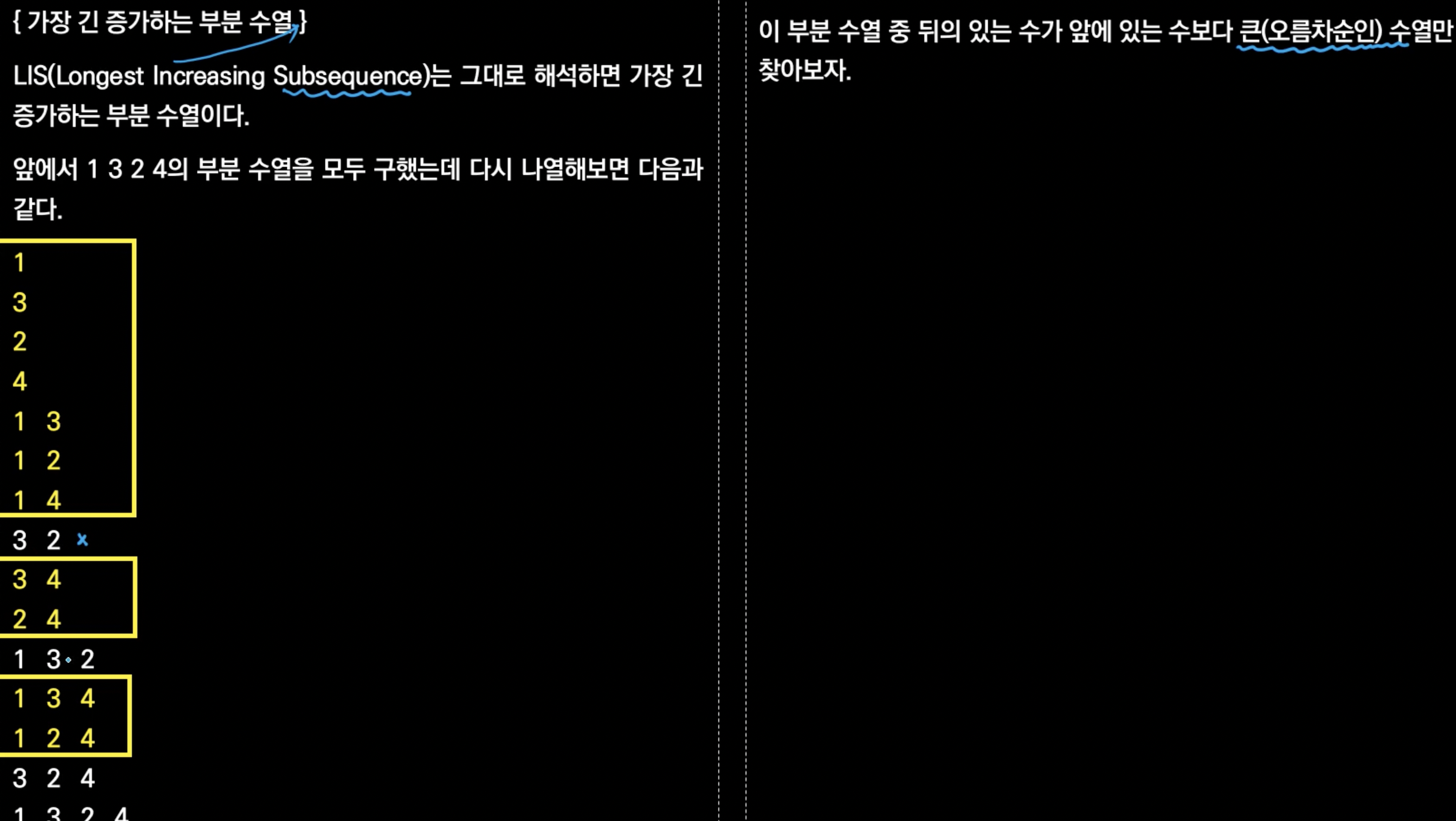
Longest Increasing Subsequence는 해석 그대로 가장 긴 증가하는 부분 수열이다. 앞에서 1 3 2 4의 부분 수열을 모두 구했는데 다시 나열해보면 다음과 같다.
예시문제

해봤는데 알고리즘식으로 풀다간 본전도 못찾는다. 무조건 경우를 나눠서 빠르게 세주어야 한다.
5번 같은 경우 100을 기준으로 왼쪽 오른쪽이 나뉘며 왼쪽에는 5개, 오른쪽에는 9개가 나온다.
해답

동적계획법
1차원 DP에서는 앞의 내용들을 이용해서 현재 위치까지의 정답을 찾는 방법을 배웠다. 이제가 표가 한 줄이 아닌 여러 줄로 나타나는 경우들에 대해서 보자. 2차원 점화식의 경우 보통 아래 두가지 컨셉 중 하나로 나온다.
① 1차원 점화식에서 사용했던 표가 두 줄 혹은 세 줄 정도 나와서 서로 영향을 주는 경우
② 가로 줄과 세로 줄이 명확한 의미가 있는 경우
①은 사실 1차원 점화식과 크게 다르지 않다
②는 문제에서 요구하는 값이 둘 이상일 경우에 나오는데, 보통 어떤 두 문자열을 비교하는 문제(LCS)나 "~인 것들 중 ~의 조건을 만족하는 것의 최댓값을 구해라" 같이 조건이 둘 이상 달린 경우에 나오게 된다. DP 문제 중 제약조건이 걸린 문제는 2차원 점화식 문제일 가능성이 높다.
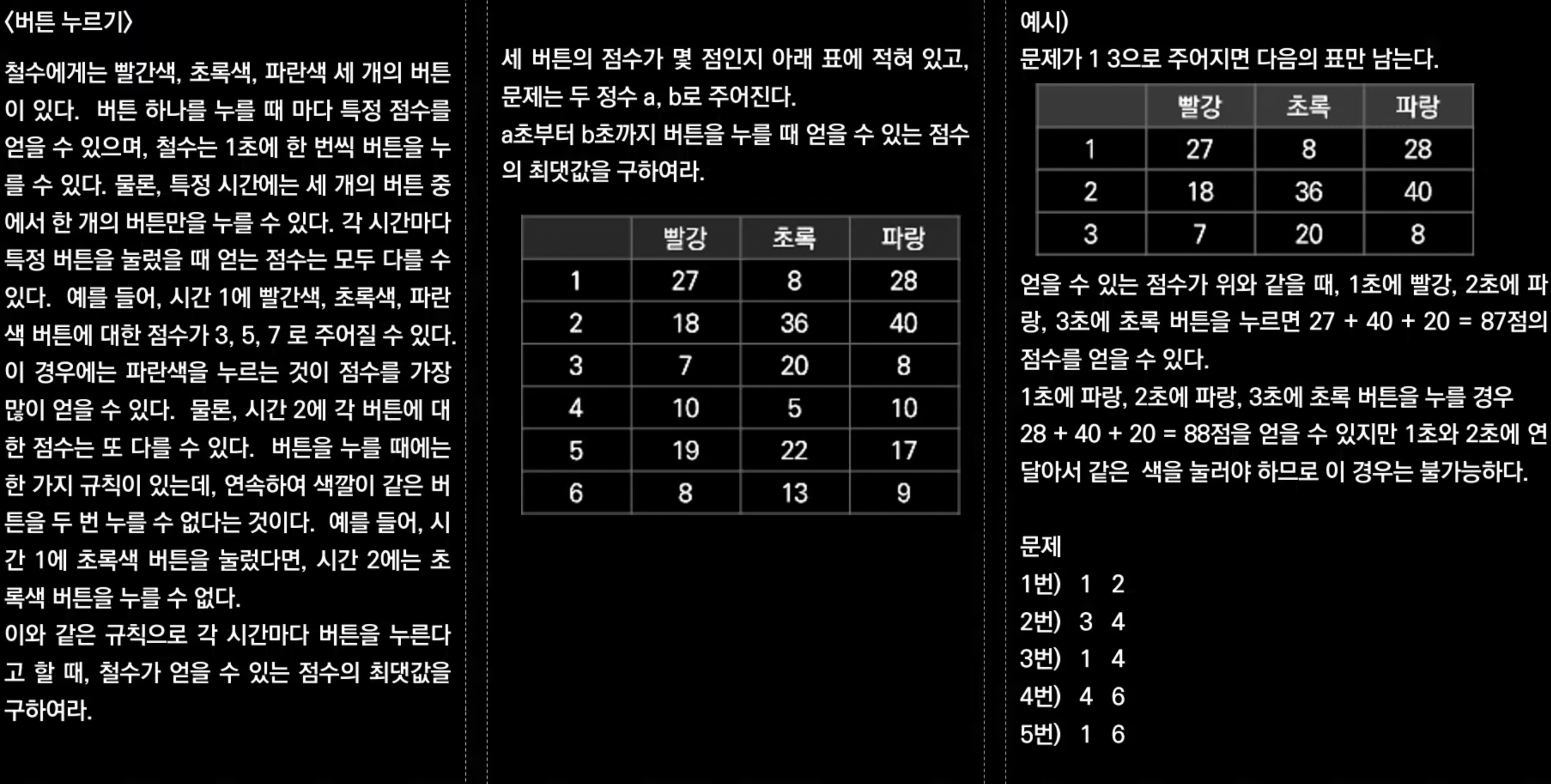
*인적성의 논리추론 문제와 비슷하다
해답

LCS
손으로 할 수 있는 문제 중에 가장 어렵다.
부분 문자열
어떤 문자열의 부분 문자열은 이 문자열에서 문자의 순서를 바꾸지 않고 몇 개를 지워서 만들 수 있는 문자열을 말한다.
예를 들어 문자열 abcd의 부분 문자열은 다음과 같다.
a / b / c / d
ab / ac / ad / bc / bd / cd
abc / abd / acd / bcd
abcd
순서를 바꾼 ca같은 것은 부분 문자열이 될 수 없다.
가장 긴 공통 부분 문자열
LCS(Longest Common Subsequence) 문제는 두 문자열 A, B가 주어질 때, A의 부분 문자열이면서 B의 부분 문자열인 문자열 중 가장 긴 것의 길이를 구하는 문제다. 예를 들어 abacd와 abca의 공통 부분 문자열은 다음과 같다.
a / b / c / aa / ab / ba / bc / ac / aba / abc
위 문자열은 모두 두 문자열의 부분 문자열이다. 이 문자열들 중 가장 긴 것은 abc, aba가 있고 길이는 3이다. 즉, LCS는 3이다.

해답


풀이

문자가 같은 곳을 표시하고 아래로 내려가면서 1을 더하지만 표시된 곳에서는 1을 더하지 않는다
2차 점화식

