2진수
우리가 사용하는 일반적인 수는 10진수, 컴퓨터가 사용하는 수는 2진수다.
10진수의 수 3124는 가장 오른쪽의 자리가 1, 그 왼쪽으로 갈수록 10씩 곱해져서 10, 100, 1000의 자리가 된다.
위와 마찬가지로 2진수의 수 11001은 가장 오른쪽 자리가 1, 그 왼쪽으로 갈수록 2씩 곱해져서 2, 4, 8, 16의 자리가 된다.
즉, 예시로 든 11001은 16이 한 개, 8이 한 개, 1이 한 개 있으므로 10진수로 표현하면 16+8+1 = 25가 된다
논리연산
비트 연산을 이해하기 위해 우선 논리 연산을 살펴보자.
여기서는 프로그래밍 언어인 c언어에 있는 논리 연산과 비트 연산의 기호를 사용한다.
논리 연산과 비트 연산 모두 다른 표기도 있으니 주의하자.
논리 피연산자 : true, false
논리 연산자: && || !
AND연산
"A가 참이고 B도 참이다"라는 말을 생각해보자. 위 말이 참이 되려면 A, B가 모두 참이어야 하고
둘 중 하나라고 거짓이면 위 명제는 거짓이다. A && B 식은 A와 B의 값에 따라 아래 표와 같이 결과가 나온다.

OR연산
"A가 참이거나 B도 참이다"라는 말을 생각해보자. 위 말이 참이 되려면 A, B가 중 하나만 참이면 되고
둘 모두 거짓이면 위 명제는 거짓이다. A || B 식은 A와 B의 값에 따라 아래 표와 같이 결과가 나온다.

NOT(!)
"A가 참이 아니다"라는 말을 생각해보자. 위 명제가 참이 되려면 A가 거짓이어야 하고
A가 참이면 위 명제는 거짓이다. !A라는 식은 A의 정보를 뒤집은 결과가 나온다.

연습 예제

*정답: true
비트연산
비트연산은 앞에서 배운 논리연산을 여러 비트에 동시에 적용하는 것이라고 보면 된다.
비트 피연산자: 2진수
비트 연산자: & | ^ ~ - < < > >
AND(&)
2진법의 수는 1101101처럼 1과 0으로 구성된다. 1인 위치를 true, 0인 위치를 false라고 생각하자.
2진법의 수 A, B에 대해 A&B는 앞에서 배운 && 연산을 같은 위치의 모든 비트에 대해 해주면 된다.
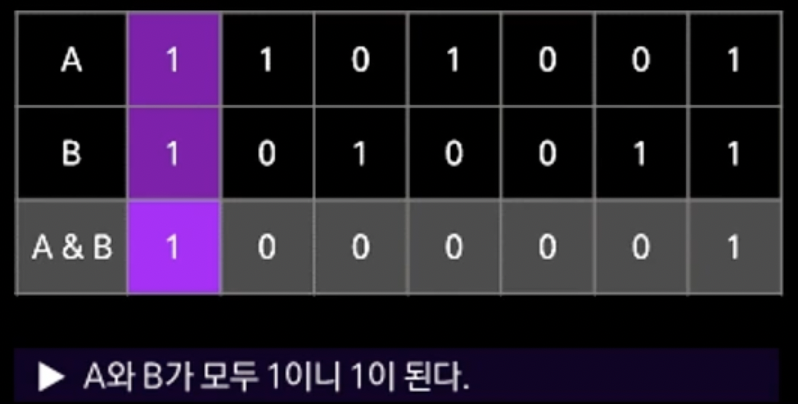
A = 1101001
B = 1010011
A&B의 결과는 다음 표의 연산으로 처리된다
OR(|)
2진법의 수는 1101101처럼 1과 0으로 구성된다. 1인 위치를 true, 0인 위치를 false라고 생각하자.
2진법의 수 A, B에 대해 A | B는 앞에서 배운 || 연산을 같은 위치의 모든 비트에 대해 해주면 된다.
A = 1101001
B = 1010011
A | B의 결과는 다음 표의 연산으로 처리된다

XOR(^)
2진법의 수는 1101101처럼 1과 0으로 구성된다. 1인 위치를 true, 0인 위치를 false라고 생각하자.
2진법의 수 A, B에 대해 A^B는 A, B의 모든 비트에 대해 서로 다른 값이 들어 있는지 판단한다
만약 어떤 위치에서 A, B값이 다르면 1이 되고, 서로 같다면 0이 된다
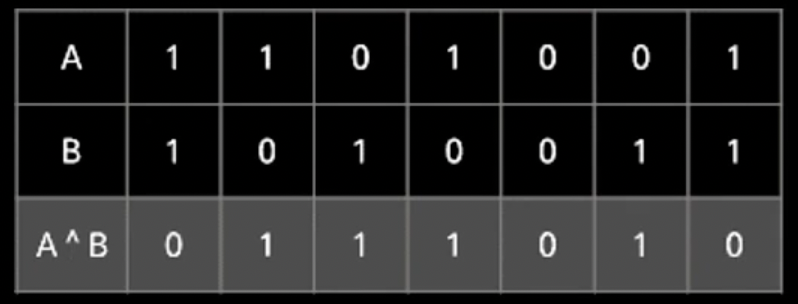
A = 1101001
B = 1010011
A ^ B의 결과는 다음 표의 연산으로 처리된다
NOT(~)
2진법의 수는 1101101처럼 1과 0으로 구성된다. 1인 위치를 true, 0인 위치를 false라고 생각하자.
2진법의 수 A에 대해 ~A는 앞에서 배운 !연산을 모든 비트에 대해 해주면 된다.
A = 1101001
~A의 결과는 다음 표의 연산으로 처리된다

※ 음수 표현법
앞서 2진법의 음수 표현법을 배웠다. 여기서는 비트연산을 이용해 음수 표현법을 나타내는 식을 배운다.
간단하게 8개의 비트를 사용하는 상황을 가정해서 -10을 구해보자.
숫자 10의 2진수 표현 : 00001010
숫자 10의 음수 표현 : 11110110
a의 음수 = -a = ~a + 1
보통 가장 왼쪽 비트가 1인 수들을 음수, 0인 수들을 양수로 본다
2^8개를 표현할 수 있다고 해서 양수 256까지 표현하는게 아닌 -128~+127을 표현하는 것이다
즉, 01111111은 양수, 10001011은 음수라고 보면 된다
(00001011이 11이니 10001011이 -11이라고 생각할 수도 있는데 그렇지 않다는 걸 주의하자)
*10001011은 -117이다. 비트를 뒤집고 양수를 계산하면 알 수 있다
부호를 의미하는 가장 왼쪽 비트를 제외하고
양수는 왼쪽부터 1이 빨리 나올수록 큰 수다
음수는 왼쪽부터 0이 빨리 나올수록 절대값이 큰 수다
왜 그런지는 변환법을 생각하면 알 수 있다
Shift 연산(<<, >>)
전체 비트를 하나씩 왼쪽 혹은 오른쪽으로 옮긴다.
왼쪽 shift 연산자는 << 이고 오른쪽 shift 연산자는 >> 이다.
01011010에 <<연산을 적용 → 10110100
이때, 가장 왼쪽에 있는 0은 8개의 비트 범위를 벗어나므로 사라지게 되고, 가장 오른쪽에 0이 추가된다.
실제 c언어 코드는 1 << 3 등의 문법을 사용하는데,
1을 왼쪽으로 3칸 shift 시킨다.
1은 00000001이므로 왼쪽으로 3칸 shift시킬 경우 00001000이 된다. 즉, 위 연산의 결과는 8이다.
오른쪽 shift(>>)는 왼쪽 shift연산과 방향만 반대이다.
가장 오른쪽 비트는 사라지고 가장 왼쪽에는 0이 추가된다.
사실 왼쪽 shift연산은 2를 곱한 것과 같은 효과, 오른쪽 shift연산은 2로 나눈 것과 같은 효과를 갖는다.
(가장 왼쪽 비트인 부호 비트를 생각하지 않을 때만 적용된다)
연습예제

*정답: 00000011 = 3

*정답: 00000010 = 2