수열
수열 문제는 어떤 수열을 만드는 규칙이 주어진다. 이 규칙을 통해 수열을 만들 때 '~번째 값은 무엇인지' 혹은 '~번째까지 중 ~한 것은 몇 개 있는지' 등을 물어보는 문제가 많이 나온다. 해결 과정은 조합과 비슷하게 한번에 묶을 수 있는 것들을 최대한 묶어서 처리하는 것이다.
문제를 풀기 전에 실제 문제를 풀 때 은근히 헷갈리는 것을 보자.


※ ~ 번째 수를 구할 때 처음 수가 포함되는 것을 염두해야 한다
첫 항과 1을 적고 그 차이를 계산한 뒤 마지막 항의 번호에 그 차이를 더하면 x번째 수가 어떤 값인지 헷갈리지 않고 구할 수 있다.
어떤 계산이든 헷갈리지 않으려면 최대한 적으면서 풀고 순서대로 보는 것을 연습하자.

해답



스택
스택은 이론 자체는 아주 단순한 자료구조다. '나중에 들어간 것이 먼저 나온다'라는 것만 기억하면 된다.
아래 그림이 스택이다. 현재 아무 정보도 없기 때문에 빈 스택이라고 보면 된다. 스택이라는 용어는 생소할 수 있으니 컵이라 생각한다.
3을 넣은 다음 5를 넣고 그 다음 8을 넣으면 다음과 같다.
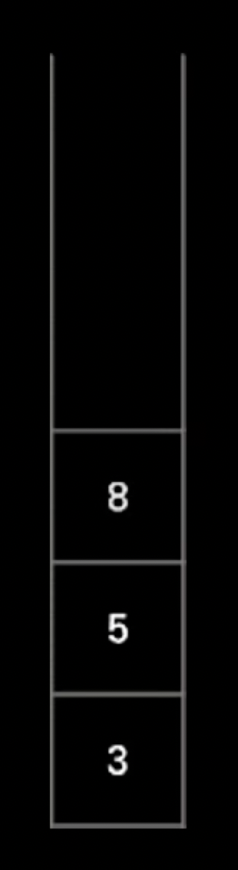

해답



그래프
그래프란 노드와 간선으로 이루어진 자료구조를 말한다. 그래프의 표현방식과 용어에 대해서는 예시를 보며 설명한다.
아래 A1~A4는 남자, B1~B4는 여자다. 각 사람에서 나가는 화살표는 그 사람이 누구를 좋아하는지 나타낸 것이라고 하자.
여기서는 모든 사람이 단 한 명의 이성을 좋아하는 상황이다. 아래 그래프에서 A1~A4와 B1~B4처럼 어떤 사람, 사물 등을
나타내는 것을 노드라고 한다. 또, 화살표처럼 노드 사이의 관계를 나타낸 것을 간선이라고 한다.

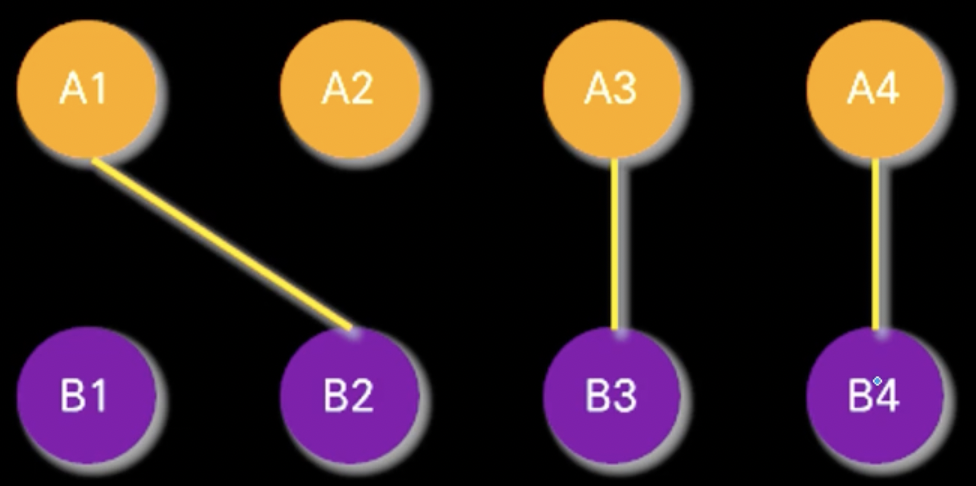
어떤 사람을 좋아하는 것은 일방적일 수 있지만 연인 같이 일방적이지 않은 관계를 나타내는 경우 간선에 방향이 없을 수 있다.
이전 페이지처럼 간선에 방향이 있는 그래프를 유향 그래프, 아래 그래프처럼 간선에 방향이 없는 그래프를 무향 그래프라고 한다.
문제를 따라 그래프를 그리면 상당히 쉽게 풀리는 경우도 있다. 숫자를 눈으로 보고 따라가는 것과 그래프를 그리고 따라가는 것은 꽤 차이가 크고 보기보다 그리는 시간이 오래 걸리지도 않으니 다음 예제처럼 그래프로 표현 가능한 문제는 그려보도록 하자.
문제를 풀 때 사이클만 그려도 된다

해답



*4번 답 42가 아닌가 싶다
동적 계획법 ( 1차원 점화식 - 단순, LIS )
영어로는 Dynamic Programming, 보통 줄여서 DP라고 부른다. (Dynamic 단어는 실제 풀이법과 관련이 없다. 동적 계획법의 고안자인 벨만은 Dynamic이라는 단어가 멋있어서 펀딩을 받기 좋은 단어라서 선택 했다고 한다.)
풀이 방법: 가장 앞의 수부터 마지막 수까지 순서대로 보면서 이전 위치들의 정보를 이용해 현재 위치까지의 정답을 구한다.
예시)
이전까지의 정보들을 보니 현재 위치는 정답이 된다/안된다.
이전까지의 정보들을 보니 현재 위치까지 최대값은 ...이다.
이전까지의 정보들을 보니 현재 위치로 오는 경우의 수는 ...이다.
이번 예시와 다음에 배울 LIS를 보며 동적 계획법이 어떤 느낌인지 살펴보자.

해답


구슬게임의 핵심은 영희가 후공이기 때문에 승리 플랜이 하나밖에 없다는 것이다.
구슬을 최소 1개에서 3개를 가져갈 수 있는데 영희는 일정한 수를 계속 만들어가는 것이다.
철수가 1개를 고르면 무조건 3을 뽑고, 2를 고르면 무조건 2를 뽑고, 3을 고르면 무조건 1개를 뽑아야한다
즉 철수가 무슨짓을 해도 만들 수 있는 총 구슬의 개수를 정하고(N) 그 크기의 배수인 구슬이 있을 때 영희는 승리할 수 있다.

