진법
10진법
우리가 일반적으로 사용하는 수는 10진법이다.
325라는 수가 있을 때, 3은 100이 3개 있다는 뜻이고, 2는 10이 2개 있다는 뜻, 5는 1이 5개 있다는 뜻이다.
다르게 표현하면 325는 3*100 + 2*10 + 5*1이다.
4325라는 수가 있다면 이 수는 4*1000 + 3*100 + 2*10 + 5*1 로 표현할 수 있다.
※ 네 자리 10진수의 표현
a*1000 + b*100 + c*10 + d*1 라는 식으로 표현 가능하다.
여기서 a는 1~9가 가능하고 나머지는 0~9가 들어올 수 있다
만약 a가 0이라면 네 자리가 아니게 되고 어떤 자리에도 10이상의 수가 들어올 수 없다
n진법
일반적으로 수를 셀 때는 10진법을 사용하지만 다른 진법을 사용하는 경우도 있다.
시간을 표현할 때 60초, 60분, 24시간을 기준으로 하는 것처럼 n진법을 사용하기도 한다.
2시 2분을 1시 62분 등으로 표현하지 않듯 60진법에서는 0보다 크거나 같고 60보다 작은 수만 사용한다.
n진법의 예시로 8진법의 수 75134라는 수가 주어졌을 때, 이 수는 다음과 같은 식으로 표현할 수 있다.
7*8^4 + 5*8^3 + 1*8^2 + 3*8^1 + 4*8^0
*여기서 ^는 XOR이 아닌 제곱
10진법 → n진법
10진법을 n진법으로 바꾸는 방법을 알아보자.
10진법의 수 1321을 8진법으로 바꾸는 과정은 다음과 같다.
1321 / 8 = 165 ‥ 1
165 / 8 = 20 ‥ 5
20 / 8 = 2 ‥ 4
2 / 8 = 0 ‥ 2
1321(10) = 2451(8)
2451(8) = 2*8^3 + 4*8^2 + 5*8^1 + 1*8^0
원리: 2*8^3 + 4*8^2 + 5*8^1 + 1*8^0 에서 8로 나눌 때마다 나오는 나머지가 곧 항이 된다
예시문제


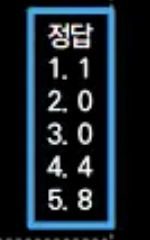
팩토리얼
팩토리얼은 1부터 n까지 많은 수를 곱하므로 보통 아주 큰 수가 된다.
예를 들어 10!만 해도 3,628,800이고 15!은 1,307,674,368,000이다.
즉, 팩토리얼 문제가 나온다면 팩토리얼을 실제로 계산하지 않고 성질을 이용해서 푸는 경우가 많다.
팩토리얼을 사용할 만한 가장 유용한 성질을 문제로 알아보자.



조합
문제에서 특별한 상황을 주고 그 상황에서 나올 수 있는 모든 경우의 수를 살펴보라는 문제가 나올 수 있다.
하지만 문제를 잘 관찰하면 그 중 여러 경우가 묶여서 한번에 처리될 수도 있다.
문제에서 봐야하는 경우가 너무 많다면 묶어서 처리하는 방법을 살펴보자.
포함배제의 원리
여러 경우를 한번에 처리할 때 주의점이 있다.
1부터 n까지의 정수 중 2의 배수도 아니고 3의 배수도 아닌 수를 찾는다고 하자.
1부터 n까지의 정수 중 2의 배수는 n/2로 구할 수 있다는 내용을 팩토리얼에서 다뤘다.
마찬가지로 1부터 n까지의 정수 중 3의 배수는 n/3으로 구할 수 있다.
그럼 1부터 n까지의 정수는 총 n개 있고, 2의 배수는 n/2개, 3의 배수는 n/3개 있으니
2의 배수도 아니고 3의 배수도 아닌 수는 n-n/2-n/3개 인 것처럼 보이지만 n-n/2-n/3+n/6이다
n=10인 경우 2의 배수도 아니고 3의 배수도 아닌 수를 생각해보자.
2의 배수: 2 4 6 8 10
3의 배수: 3 6 9
6이 겹치는 걸 확인할 수 있다.
즉, n-n/2-n/3을 하면 6이 두 번 빠지게 되므로 그만큼을 다시 더해줘야 한다.





shift연산을 활용해 2진수로 바꾼다음 푼다. 아니면 주어진 숫자를 역순으로 분해한다
