Devjo의 코딩

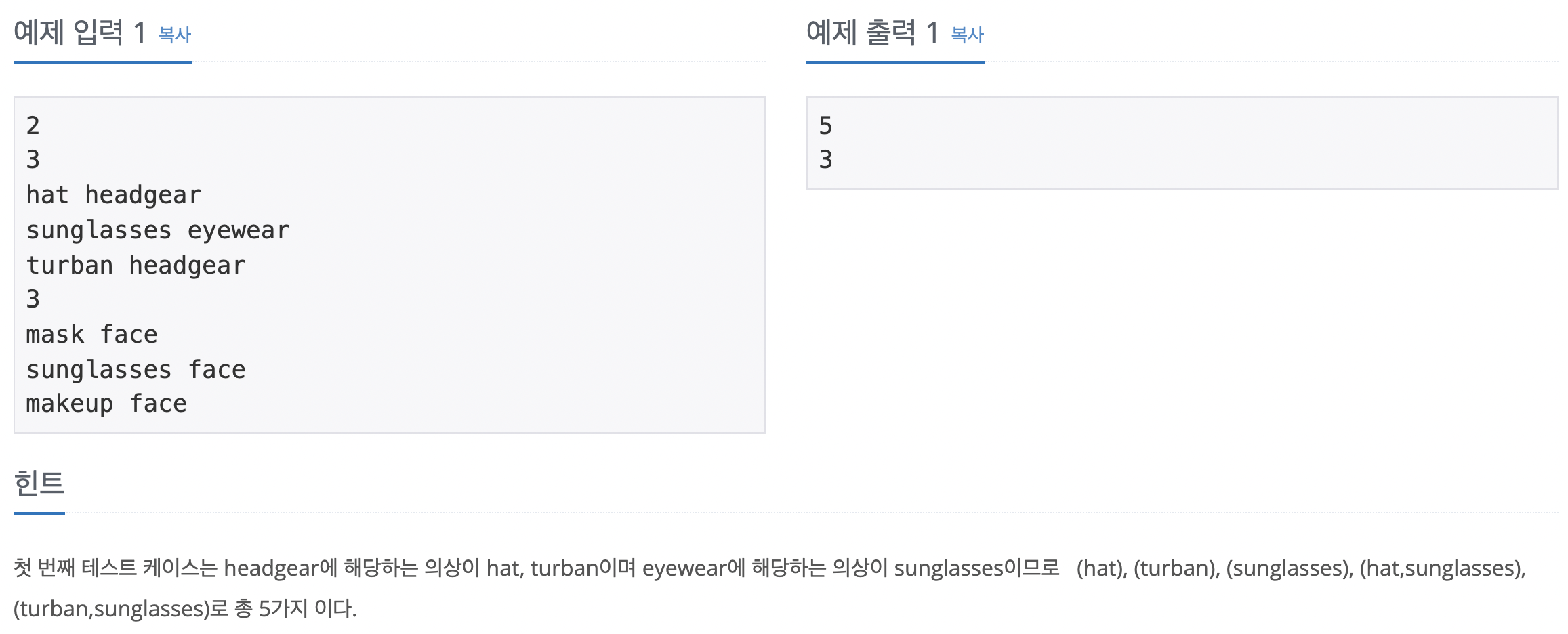
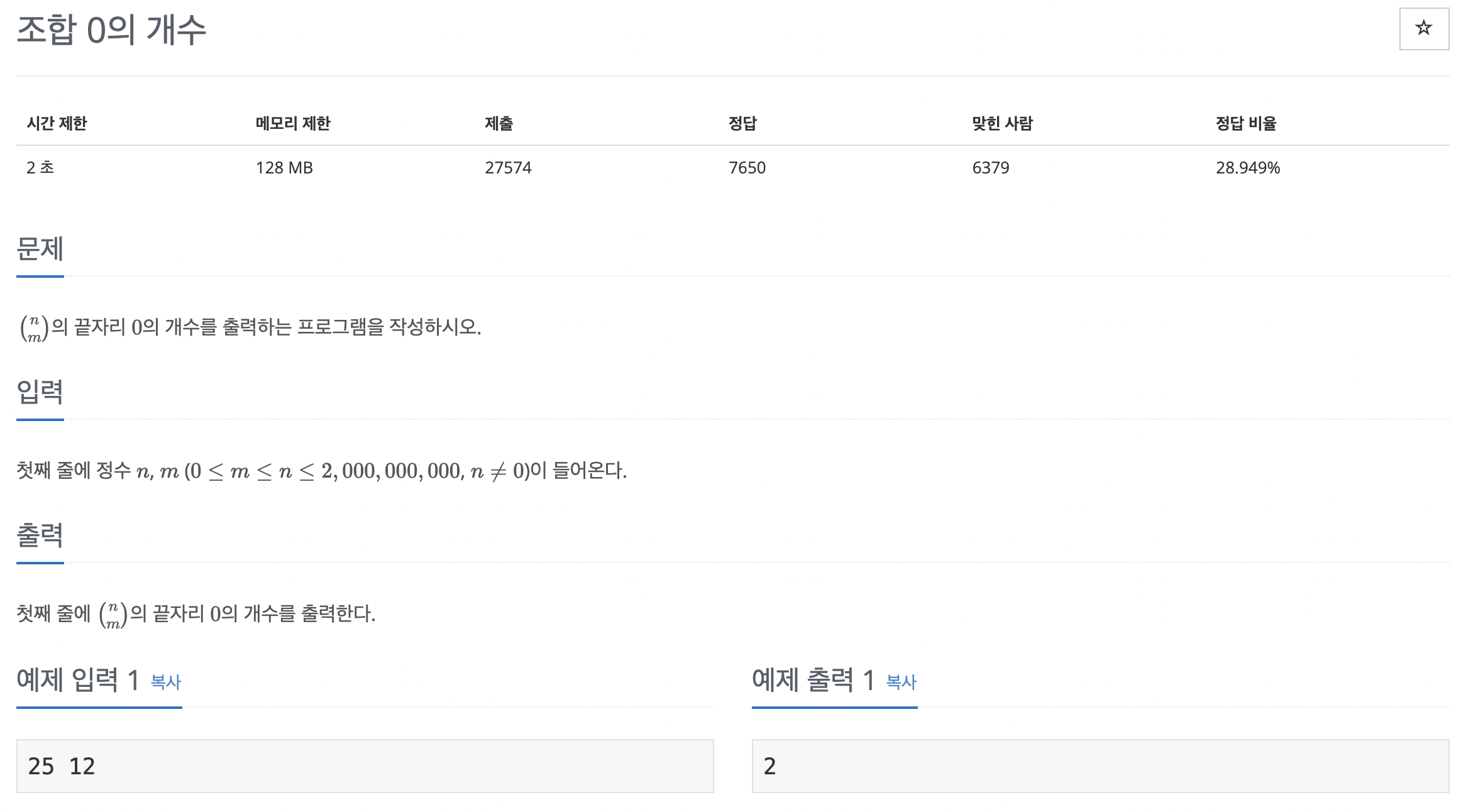
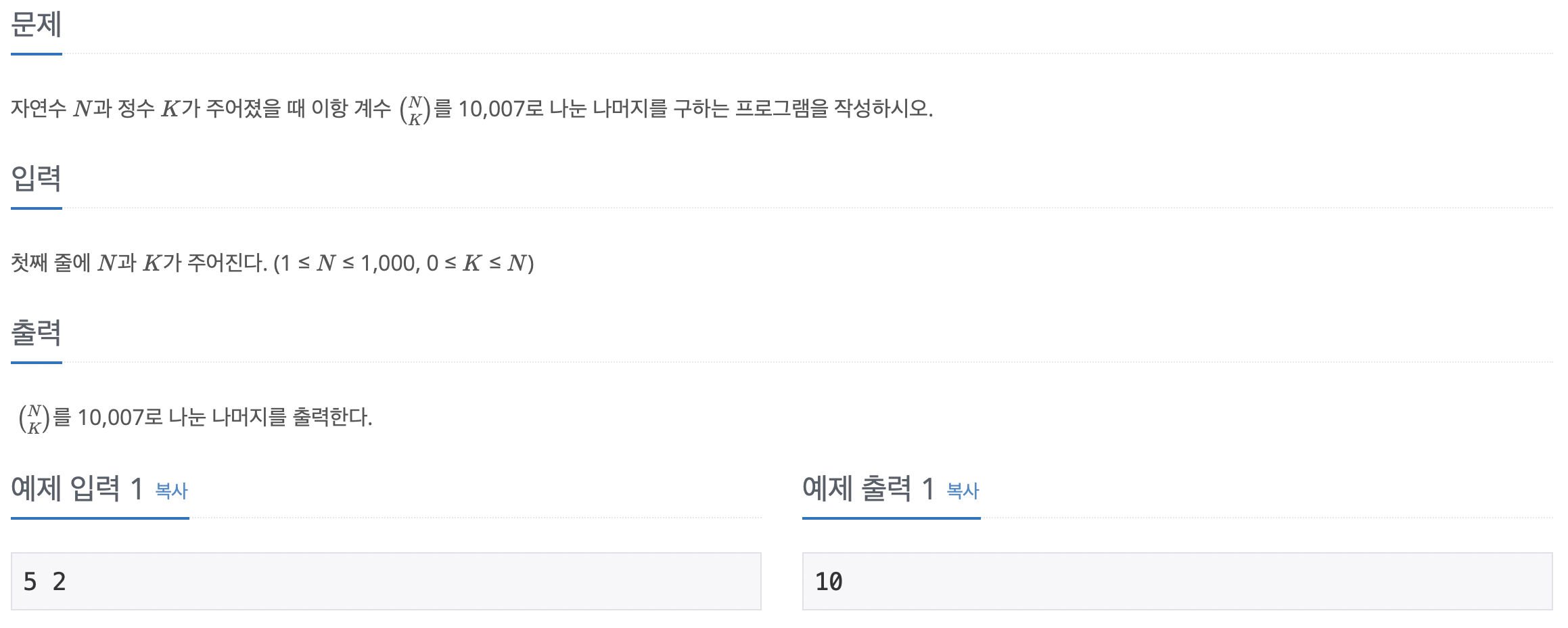
랜선 자르기 2 초 128 MB 92515 21166 13953 20.920% 문제 집에서 시간을 보내던 오영식은 박성원의 부름을 받고 급히 달려왔다. 박성원이 캠프 때 쓸 N개의 랜선을 만들어야 하는데 너무 바빠서 영식이에게 도움을 청했다. 이미 오영식은 자체적으로 K개의 랜선을 가지고 있다. 그러나 K개의 랜선은 길이가 제각각이다. 박성원은 랜선을 모두 N개의 같은 길이의 랜선으로 만들고 싶었기 때문에 K개의 랜선을 잘라서 만들어야 한다. 예를 들어 300cm 짜리 랜선에서 140cm 짜리 랜선을 두 개 잘라내면 20cm는 버려야 한다. (이미 자른 랜선은 붙일 수 없다.) 편의를 위해 랜선을 자르거나 만들 때 손실되는 길이는 없다고 가정하며, 기존의 K개의 랜선으로 N개의 랜선을 만들 수 없는 경우..

숫자 카드 2 1 초 256 MB 49590 17969 12742 35.725% 문제 숫자 카드는 정수 하나가 적혀져 있는 카드이다. 상근이는 숫자 카드 N개를 가지고 있다. 정수 M개가 주어졌을 때, 이 수가 적혀있는 숫자 카드를 상근이가 몇 개 가지고 있는지 구하는 프로그램을 작성하시오. 입력 첫째 줄에 상근이가 가지고 있는 숫자 카드의 개수 N(1 ≤ N ≤ 500,000)이 주어진다. 둘째 줄에는 숫자 카드에 적혀있는 정수가 주어진다. 숫자 카드에 적혀있는 수는 -10,000,000보다 크거나 같고, 10,000,000보다 작거나 같다. 셋째 줄에는 M(1 ≤ M ≤ 500,000)이 주어진다. 넷째 줄에는 상근이가 몇 개 가지고 있는 숫자 카드인지 구해야 할 M개의 정수가 주어지며, 이 수는 공..

수 찾기 1 초 128 MB 111974 33128 21892 30.185% 문제 N개의 정수 A[1], A[2], …, A[N]이 주어져 있을 때, 이 안에 X라는 정수가 존재하는지 알아내는 프로그램을 작성하시오. 입력 첫째 줄에 자연수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1 ≤ M ≤ 100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들이 A안에 존재하는지 알아내면 된다. 모든 정수의 범위는 -231 보다 크거나 같고 231보다 작다. 출력 M개의 줄에 답을 출력한다. 존재하면 1을, 존재하지 않으면 0을 출력한다. 풀이 정수의 범위가 2의 31승으로 매우 크다. 즉 카운팅 배열..

검문 1 초 128 MB 23840 4684 3687 21.292% 문제 트럭을 타고 이동하던 상근이는 경찰의 검문을 받게 되었다. 경찰은 상근이가 운반하던 화물을 하나하나 모두 확인할 것이기 때문에, 검문하는데 엄청나게 오랜 시간이 걸린다. 상근이는 시간을 때우기 위해서 수학 게임을 하기로 했다. 먼저 근처에 보이는 숫자 N개를 종이에 적는다. 그 다음, 종이에 적은 수를 M으로 나누었을 때, 나머지가 모두 같게 되는 M을 모두 찾으려고 한다. M은 1보다 커야 한다. N개의 수가 주어졌을 때, 가능한 M을 모두 찾는 프로그램을 작성하시오. 입력 첫째 줄에 종이에 적은 수의 개수 N이 주어진다. (2 ≤ N ≤ 100) 다음 줄부터 N개 줄에는 종이에 적은 수가 하나씩 주어진다. 이 수는 모두 1보다 ..

사장님 도박은 재미로 하셔야 합니다 1 초 512 MB 189 155 115 79.861% 문제 영국에는 스티븐 제라드라는 전설의 야바위꾼이 있다. 영국으로 여행을 떠난 윤성이는 스티븐 제라드를 만나게 되었다. 이 전설의 야바위꾼이 진행하는 야바위는 널리 알려진 방식과 동일하다. 3개의 컵과 하나의 공을 사용해 임의의 한 컵에 공을 넣고 무작위로 컵들의 위치를 바꾼다. 야바위꾼이 정한 특정 순간에 위치 변경을 멈추게 되는데 그 순간 관객이 공의 위치를 찾으면 돈을 받을 수 있다. 스티븐 제라드가 공의 위치를 찾았을 때 베팅한 돈의 10배를 주겠다 제안하자 윤성이는 솔깃해져 게임에 참여하게 되었다. 전설의 야바위꾼의 빠른 손놀림에 윤성이는 단 한번도 공의 위치를 찾지 못했고, 결국 윤성이는 배팅을 계속하다..

패션왕 신해빈 1 초 128 MB 12554 6774 5871 54.772% 문제 해빈이는 패션에 매우 민감해서 한번 입었던 옷들의 조합을 절대 다시 입지 않는다. 예를 들어 오늘 해빈이가 안경, 코트, 상의, 신발을 입었다면, 다음날은 바지를 추가로 입거나 안경대신 렌즈를 착용하거나 해야한다. 해빈이가 가진 의상들이 주어졌을때 과연 해빈이는 알몸이 아닌 상태로 며칠동안 밖에 돌아다닐 수 있을까? 입력 첫째 줄에 테스트 케이스가 주어진다. 테스트 케이스는 최대 100이다. 각 테스트 케이스의 첫째 줄에는 해빈이가 가진 의상의 수 n(0 ≤ n ≤ 30)이 주어진다. 다음 n개에는 해빈이가 가진 의상의 이름과 의상의 종류가 공백으로 구분되어 주어진다. 같은 종류의 의상은 하나만 입을 수 있다. 모든 문자열..

풀이 끝자리 0의 개수는 5와 2의 곱의 개수로 만들어진다. 하지만 2의 개수와 5의 개수만 세어주면된다. 5!은 1개 10!은 2개 15!은 3개 20!은 4개 25!은 6개다. 이런식으로 n!에 대해 5의 개수를 계산하는 메소드를 만들고 입력한 N, M에 대해 N! M! (N-M)!의 5의 개수를 구한다 N!의 5의 개수에서 나머지 둘을 빼주면 끝자리 0의 개수를 구할 수 있다. 반례 - N=5, M=4 2의 개수가 충분하다고 생각할 수 있지만 n=5 m=4가 입력된다면 각각의 5의 배수는 1개, 0개 이므로 1이라는 결과값을 낸다. 하지만 5! ÷ 4!은 5이며 10이 되지 않는다. 이는 둘에서 발견되는 2의 배수의 개수를 고려하지 않았기 때문이다. 위에서 만들어준 논리와 같은 2의 배수의 개수를 ..

이항 계수 2 1 초 256 MB 33293 12522 9832 38.451% 풀이 팩토리얼을 메소드를 만들고 숫자 데이터를 Double로 받아 연산해도 결과값은 NaN이 나온다. 1000까지 곱하기 때문에 Double의 표현 자리수를 넘어가는데 이를 방지하기 위해 중간중간 곱하기마다 10007로 나누어 숫자 크기를 줄여주어야 한다(모듈러 연산). 파스칼의 삼각형 처배열을 이용한 풀이를 생각했지만 파스칼의 삼각형 풀이보다 효율적이지 못한 것 같다. 이항 계수의 성질과 dp를 이용하면 빠르게 풀이할 수 있다. (N K)=(N-1 K-1) + (N-1 K) N을 1000까지 사용하므로 [1001][1001] 배열을 만들고 dp를 적용한다. K=0일 때와 N=K일 때 dp의 값은 1이다. import java..

이항 계수 1 1 초 256 MB 26624 17107 14770 64.442% 풀이 입력값 N, K에 대하여 이항 계수 (N K)의 값은 N!/K!(N-K)! 이다. 팩토리얼 메소드를 활용한다. import java.util.*; public class Main { static int Fac(int N) { if(N

문제) 12와 20의 최대공약수를 구하시오 어떻게 푸시나요? ​ 보통 나눗셈을 합니다 최대공약수 = 2X2 = 4​ 하지만 주어진 두 수가 엄청 크다면 어떤 수로 나눠야할지 일일히 찾아야하기 때문에 컴퓨터 연산에서는 비효율적입니다 ​ ​ 최대공약수 A와 B의 나머지 연산으로 최대공약수를 구한다 ​ 두 수(12, 20)만으로 최대공약수를 구해봅시다​ 20 % 12 = 8 (20을 12로 나눈 나머지) 12 % 8 = 4 (12를 8로 나눈 나머지) 8 % 4 = 0 (나머지가 0일 때 그 수는 최대공약수) ​ 논리가 매우 단순해졌죠??​ 메소드로 만들면 다음과 같습니다 static int GCD(int A, int B) { //B를 A로 나눈 나머지를 구합니다 if(A==0)return B; // 마지막 ..