창고 다각형
| 2 초 | 128 MB | 6650 | 2788 | 2215 | 43.338% |
문제
N 개의 막대 기둥이 일렬로 세워져 있다. 기둥들의 폭은 모두 1 m이며 높이는 다를 수 있다. 이 기둥들을 이용하여 양철로 된 창고를 제작하려고 한다. 창고에는 모든 기둥이 들어간다. 이 창고의 지붕을 다음과 같이 만든다.
- 지붕은 수평 부분과 수직 부분으로 구성되며, 모두 연결되어야 한다.
- 지붕의 수평 부분은 반드시 어떤 기둥의 윗면과 닿아야 한다.
- 지붕의 수직 부분은 반드시 어떤 기둥의 옆면과 닿아야 한다.
- 지붕의 가장자리는 땅에 닿아야 한다.
- 비가 올 때 물이 고이지 않도록 지붕의 어떤 부분도 오목하게 들어간 부분이 없어야 한다.
그림 1은 창고를 옆에서 본 모습을 그린 것이다. 이 그림에서 굵은 선으로 표시된 부분이 지붕에 해당되고, 지붕과 땅으로 둘러싸인 다각형이 창고를 옆에서 본 모습이다. 이 다각형을 창고 다각형이라고 하자.
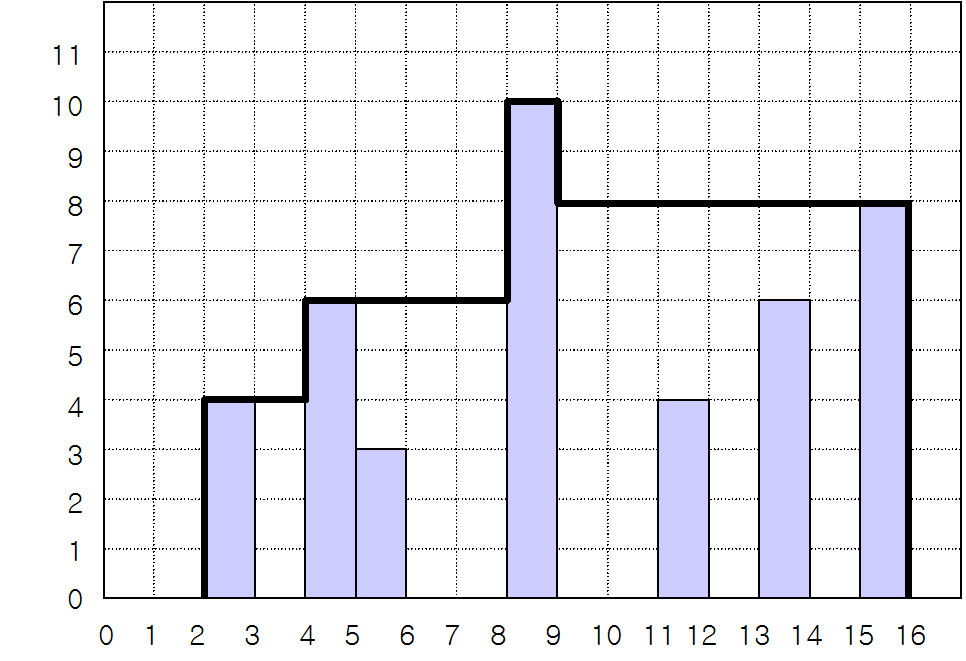
그림1 . 기둥과 지붕(굵은 선)의 예
창고 주인은 창고 다각형의 면적이 가장 작은 창고를 만들기를 원한다. 그림 1에서 창고 다각형의 면적은 98 ㎡이고, 이 경우가 가장 작은 창고 다각형이다.
기둥들의 위치와 높이가 주어질 때, 가장 작은 창고 다각형의 면적을 구하는 프로그램을 작성하시오.
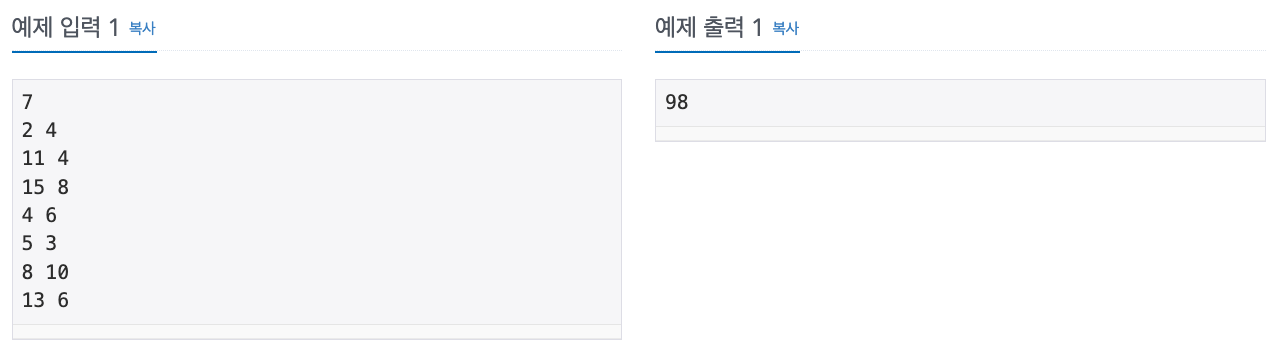
입력
첫 줄에는 기둥의 개수를 나타내는 정수 N이 주어진다. N은 1 이상 1,000 이하이다. 그 다음 N 개의 줄에는 각 줄에 각 기둥의 왼쪽 면의 위치를 나타내는 정수 L과 높이를 나타내는 정수 H가 한 개의 빈 칸을 사이에 두고 주어진다. L과 H는 둘 다 1 이상 1,000 이하이다.
출력
첫 줄에 창고 다각형의 면적을 나타내는 정수를 출력한다.
풀이1
최대값을 기준으로 왼쪽 구역은 높이가 증가해야만하고 오른쪽 구역은 감소해야만 합니다.
입력 값을 받을 때 최대값과 그 때의 index를 구하고 그 indexd에 도달할 때까지는 증가만하면서 면적을 더해주고 다시 끝에서부터 index에 거꾸로 도달할 때까지 증가만하면서 면적을 더해줍니다.
L과 H모두 1000이하
x 좌표가 1억이라면 수학적인 풀이로 진행해야합니다. 하지만 1000개므로 갱신하면서 채워넣기가 가능합니다
최대값을 기준으로 양쪽에서 출발
왼쪽 끝에서 출발, 오른쪽 끝에서 각각 출발해 중앙에 있는 최대값으로 도달합니다.
출발하면서 최대값을 만나면 최대값이 있는 중앙까지 모두 색칠해버립니다.
1차원 배열로 구현했기 때문에 높이만 바꿔줍니다.
# 입력 부분
area = list(0 for i in range(1001))
N = int(input())
rod = [list(map(int,input().split())) for i in range(N)]
rod.sort(key=lambda x: x[0]) # 2차원 정렬
MAX = idx = idx_pic = 0 # 막대기 최대값, 그 때 인덱스 (배열, 그림)
for i in range(N):
if rod[i][1] > MAX:
MAX = rod[i][1] # 막대기 중 최대값 가장 먼저 나타나는 지점
idx = i # 최대일 때, 리스트상 인덱스
idx_pic = rod[i][0] # 최대일 때 그림상 인덱스
max = 0 # 순간 순간의 최대값
for i in range(idx+1): # [2,4] [4, 6]
if max < rod[i][1]:
max = rod[i][1]
for j in range(rod[i][0],idx_pic+1):
area[j] = max
rod.reverse() # 뒤집고 거꾸로 진행
max = 0 # 초기화
for i in range(len(rod)-idx):
if max < rod[i][1]:
max = rod[i][1]
for j in range(idx_pic,rod[i][0]+1):
area[j] = max
print(sum(area))
'Study > Baekjoon' 카테고리의 다른 글
| [Python] Baekjoon2578: 빙고, 오답이 될 수 있는 경우는? (0) | 2022.01.29 |
|---|---|
| [Python] Baekjoon2559: 수열 (0) | 2022.01.29 |
| [Python] Baekjoon2529: 부등호 (0) | 2022.01.28 |
| [Python]Baekjoon18870: 좌표 압축 (0) | 2022.01.28 |
| [Python]Baekjoon18870: 좌표 압축 (0) | 2022.01.28 |