문제
다음 소스는 N번째 피보나치 수를 구하는 C++ 함수이다.
int fibonacci(int n) {
if (n == 0) {
printf("0"); return 0; }
else if (n == 1) {
printf("1"); return 1; }
else { return fibonacci(n‐1) + fibonacci(n‐2); } }
fibonacci(3)을 호출하면 다음과 같은 일이 일어난다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1) (첫 번째 호출)을 호출한다.
- fibonacci(2)는 fibonacci(1) (두 번째 호출)과 fibonacci(0)을 호출한다.
- 두 번째 호출한 fibonacci(1)은 1을 출력하고 1을 리턴한다.
- fibonacci(0)은 0을 출력하고, 0을 리턴한다.
- fibonacci(2)는 fibonacci(1)과 fibonacci(0)의 결과를 얻고, 1을 리턴한다.
- 첫 번째 호출한 fibonacci(1)은 1을 출력하고, 1을 리턴한다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1)의 결과를 얻고, 2를 리턴한다.
1은 2번 출력되고, 0은 1번 출력된다. N이 주어졌을 때, fibonacci(N)을 호출했을 때, 0과 1이 각각 몇 번 출력되는지 구하는 프로그램을 작성하시오.
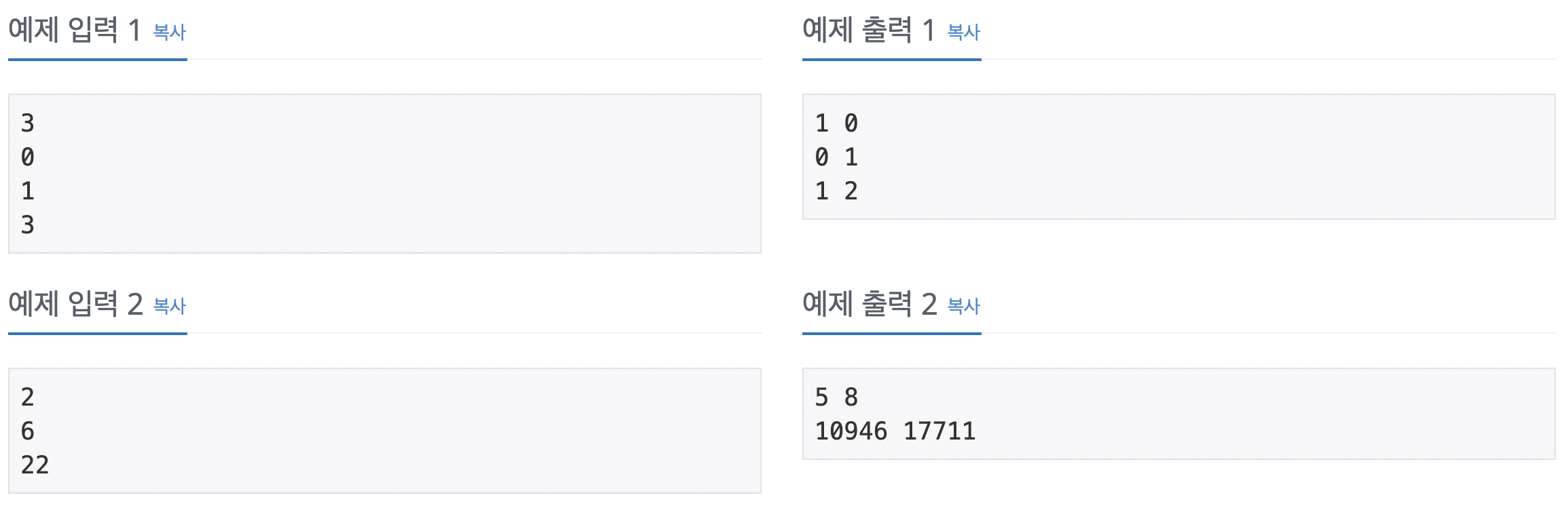
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다.
각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. N은 40보다 작거나 같은 자연수 또는 0이다.
출력
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
풀이
시간 제한이 0.25초로 매우 짧다. 일반적으로 피보나치 수열을 40항까지 매번 계산하다간 제한 시간 안에 연산할 수 없을 것이다.
동적 계획법(DP-Dynamic Programming)을 사용한다. 이미 구한 값에 대해서 기록하며 계산 횟수를 줄여야 한다.
N의 제한 조건이 0<= N <=40이고 0항과 1항이 몇 번 시행해야하는지 구하므로 이중배열 [41][2]를 사용한다.
계산이 안되어있는 부분은 확실하게 표현되야 하므로 null값을 초기값으로 가지는 Integer로 배열을 만들어준다(int는 초기값 0)
배열에 기록하며 값이 없는 경우만 다시 계산하여 이전 계산을 되풀이 하지 않도록 한다.
import java.io.*;
public class Main {
static Integer[][] dp = new Integer[41][2]; //[41][2]크기의 이중배열 선언
//int가 아닌 데이터타입을 Integer로 설정하여 초기값을 null로 설정한다
static Integer[] fibonacci(int N) {
if(dp[N][0]==null || dp[N][1]==null) { //값이 없는 경우만 계산을 실시한다
dp[N][0]= fibonacci(N-1)[0] + fibonacci(N-2)[0];
dp[N][1]= fibonacci(N-1)[1] + fibonacci(N-2)[1];
}
return dp[N];
// 이중배열에서 값을 나눠 계산해주기 위해 [N]을 먼저 적어준다
// fibonacci(N-1)은 dp[N-1]을 결과값으로 반환하는데
// fibonacci(N-1)[0] 라는 표현을 통해 dp[N-1][0]을 표현할 수 있다.
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//초항들을 적어준다
dp[0][0] = 1; dp[0][1] = 0; //0항에서 호출된 0항의 수=1, 0항에서 사용된 1항의 수=0
dp[1][0] = 0; dp[1][1] = 1; //1항에서 호출된 0항의 수=0, 0항에서 사용된 1항의 수=1
int T = Integer.parseInt(br.readLine());
while(T-->0) {
int N = Integer.parseInt(br.readLine());
fibonacci(N);
System.out.println(dp[N][0]+" "+dp[N][1]);
}}}
'Study > Baekjoon' 카테고리의 다른 글
| Baekjoon1904: 01타일 (0) | 2021.10.26 |
|---|---|
| Baekjoon9184: 신나는 함수 실행 (0) | 2021.10.25 |
| Baekjoon5430: AC (0) | 2021.10.24 |
| Baekjoon1021: 회전하는 큐, 덱의 배열화 (0) | 2021.10.24 |
| Baekjoon10866: 덱 (0) | 2021.10.24 |