직사각형
| 1 초 | 128 MB | 4049 | 1009 | 850 | 34.553% |
문제
2차원 격자공간에 두 개의 꼭짓점 좌표로 표현되는 직사각형이 있다. 직사각형은 아래와 같이 왼쪽 아래 꼭짓점 좌표 (x, y)와 오른쪽 위 꼭짓점 좌표 (p, q)로 주어진다.

이 문제에서 모든 직사각형은 두 꼭짓점의 좌표를 나타내는 4개의 정수 x y p q 로 표현된다. 단 항상 x<p, y<q 이다. 예를 들어 위 그림에 제시된 직사각형이라면 아래와 같이 표현된다.
3 2 9 8
두 개의 직사각형은 그 겹치는 부분의 특성에 따라 다음 4가지 경우로 분류될 수 있다.
먼저 두 직사각형의 겹치는 부분이 직사각형인 경우이다. 아래 그림(a)는 공통부분이 직사각형인 경우의 3가지 예를 보여준다,

그림 (a)
또는 겹치는 부분이 아래 그림 (b)와 같이 선분이 될 수도 있고, 그림 (c)와 같이 점도 될 수 있다.

그림 (b)
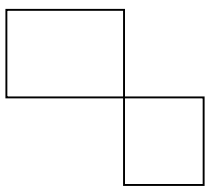
그림 (c)
마지막으로 아래 그림 (d)와 같이 공통부분 없이 두 직사각형이 완전히 분리된 경우도 있다.

그림 (d)
여러분은 두 직사각형의 겹치는 부분이 직사각형인지, 선분인지, 점인지, 아니면 전혀 없는 지를 판별해서 해당되는 코드 문자를 출력해야 한다.
공통부분의 특성코드 문자| 직사각형 | a |
| 선분 | b |
| 점 | c |
| 공통부분이 없음 | d |
입력
4개의 줄로 이루어져 있다. 각 줄에는 8개의 정수가 하나의 공백을 두고 나타나는데, 첫 4개의 정수는 첫 번째 직사각형을, 나머지 4개의 정수는 두 번째 직사각형을 각각 나타낸다. 단 입력 직사각형의 좌표 값은 1이상 50,000 이하의 정수로 제한된다.
출력
4개의 각 줄에 주어진 두 직사각형의 공통부분을 조사해서 해당하는 코드 문자를 출력파일의 첫 4개의 줄에 각각 차례대로 출력해야 한다.

풀이
한 사각형을 고정시키고 나머지 사각형의 끝점으로 검사하면 되지 않을까 생각해봤지만 다음 반례가 있었습니다.

위 처럼 서로의 점이 각 사각형 안에 포함되지 않은 경우입니다.
각 선분으로 서로의 관계를 정의
그래서 2개의 사각형 각각의 x 선분과 y선분을 통해 관계를 정의해줬습니다
서로 x 선분과 y선분을 비교할 때 선분의 위치관계를 다음과 같이 정의할 수 있습니다.
i) 서로의 선분이 겹침
ii) 서로의 선분이 한 점에서 만남
iii) 서로의 선분이 만나지 않음
선분의 관계를 이용한 겹침 판단
1) 두 사각형이 직사각형을 만들면서 만남: 서로의 x 선분과 y 선분이 모두 겹침
2) 두 사각형이 선에서 만남: x선분과 y선분 중 하나의 선분이 한 점에서 만남
3) 두 사각형이 점에서 만남: x선분과 y선분 모두가 한 점에서 만남
4) 두 사각형이 만나지 않음: x선분과 y선분 모두 만나지 않음
def line(x1,x2,x3,x4): # 두 선분의 관계 판단
# 조건: x1 < x2 , x3 < x4
if x2 < x3 or x4 < x1: # 만나지 않음
return 0
elif x2 == x3 or x1 == x4: # 한 점에서 만남
return 1
else:
return 2 # 겹침
for i in range(4):
rec = list(map(int,input().split()))
# x1 y1 x2 y2 x1 y1 x2 y2
# 0 1 2 3 4 5 6 7
relationX = line(rec[0],rec[2],rec[4],rec[6])
relationY = line(rec[1],rec[3],rec[5],rec[7])
result = relationX*relationY # 곱한 결과값 계산
if result == 0:
print('d')
elif result == 1:
print('c')
elif result == 2:
print('b')
else:
print('a')
'Study > Baekjoon' 카테고리의 다른 글
| [Python] Baekjoon11729: 하노이 탑 이동 순서 (0) | 2022.01.31 |
|---|---|
| [Python] Baekjoon1929: 소수 구하기 (0) | 2022.01.31 |
| [Python] Baekjoon2477: 참외밭 (0) | 2022.01.30 |
| [Python] Baekjoon2578: 빙고, 오답이 될 수 있는 경우는? (0) | 2022.01.29 |
| [Python] Baekjoon2559: 수열 (0) | 2022.01.29 |