행렬 제곱
| 1 초 | 256 MB | 15959 | 5554 | 4450 | 34.247% |
문제
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
입력
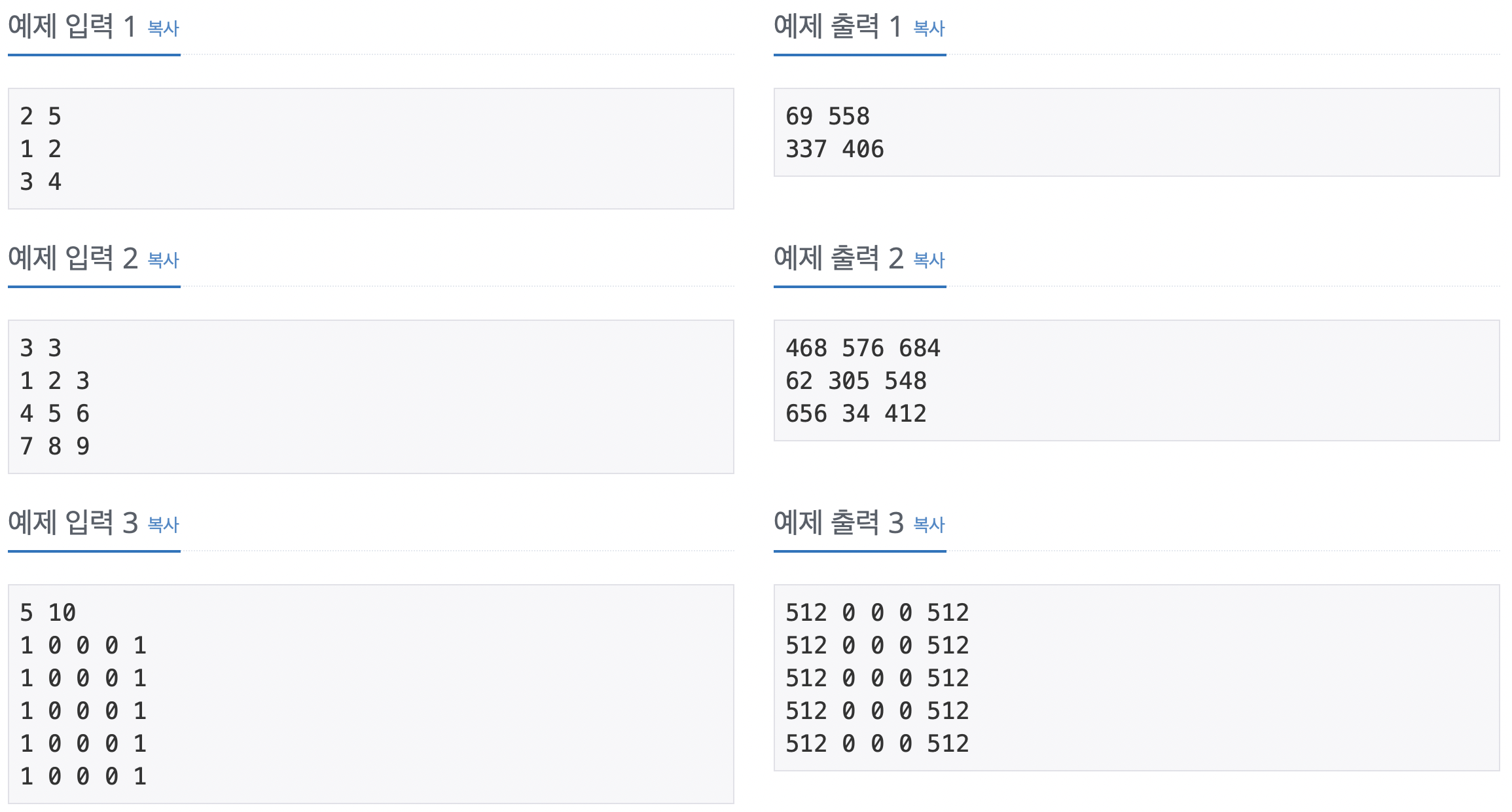
첫째 줄에 행렬의 크기 N과 B가 주어진다. (2 ≤ N ≤ 5, 1 ≤ B ≤ 100,000,000,000)
둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다. 행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다.
출력
첫째 줄부터 N개의 줄에 걸쳐 행렬 A를 B제곱한 결과를 출력한다.
풀이
B로 10을 입력받으면 어떻게 곱해야할까? 1629번 백준문제 곱셈에서 사용한 개념을 사용하면 다음과 같다
A의 10승
= 5승 x 5승
= (2승x2승x1승)x(2승x2승+1승)
= 1승x1승x1승x1승x1승x1승x1승x1승x1승x1승짝수인 경우 그냥 나눠주면 되지만
5승처럼 홀수 형태이면 5를 일단 나눈 2승을 서로 곱하고(2승x2승) 나머지 1승을 따로 곱해주어야한다(x1승).
메소드의 형태
B의 크기가 천 억 단위까지가므로 Long을 사용한다. 또한 연산 결과를 계속 1000으로 나눈 나머지로 유지한다(모듈러 연산).
분할정복을 수행하며 메소드의 리턴값은 NxN 배열의 값이어야 바로 정답으로 사용할 수 있다.
static int[][] powerMatrix(long B) // 행렬의 거듭제곱 메소드, B가 워낙 크므로 long재귀호출 값을 미리 받기
행렬의 곱셈을 위해서 미리 이전 항의 배열을 저장해놓아야한다.
int[][] before = powerMatrix(B/2);계산
이전 항의 배열을 가져온다음 그 값을 서로 곱해주어야 한다.
행렬의 곱을 반복문으로 표현하면 다음과 같다
for(int i=0;i<N;i++) {
for(int j=0;j<N;j++) {
for(int k=0;k<N;k++) {
결과행렬[i][j] += 행렬1[i][k] * 행렬2[k][j];
}
}
}이를 활용해 방금 미리 값을 가져온 이전항의 배열 before[N][N]을 서로 곱해주어 임시배열 tmp[N][N]에 넣어주고
그 tmp 배열을 결과값(리턴값)으로 반환하는 것이다.
B를 2로 나눈 나머지
여기서 B가 짝수인 경우 tmp를 그냥 리턴하면 되지만
B가 홀수인 경우 나눴을 때 사라진 1만큼을 더 곱해줘야하므로 입력값으로 받았던 A행렬을 tmp에 한 번 더 곱해준다.
import java.util.Scanner;
public class Main {
static int[][] A;
static int N;
static int[][] powerMatrix(long B) {
if(B==1) {
return A;
}
int[][] before = powerMatrix(B/2);
int[][] tmp = new int[N][N];
for(int i=0;i<N;i++) {
for(int j=0;j<N;j++) {
for(int k=0;k<N;k++) {
tmp[i][j]+=before[i][k]*before[k][j]%1000;
}
}
}
if(B%2==0) {
return tmp;
}else {
int[][] tmp2 = new int[N][N];
for(int i=0;i<N;i++) {
for(int j=0;j<N;j++) {
for(int k=0;k<N;k++) {
tmp2[i][j]+=tmp[i][k]*A[k][j]%1000;
}
}
}
return tmp2;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
A=new int[N][N];
long B = sc.nextLong();
for(int i=0;i<N;i++) {
for(int j=0;j<N;j++) {
A[i][j]=sc.nextInt();
}
}
int[][] answer = powerMatrix(B);
for(int i=0;i<N;i++) {
for(int j=0;j<N;j++) {
System.out.print(answer[i][j]%1000+" ");
}
System.out.println();
}
}}
'Study > Baekjoon' 카테고리의 다른 글
| Baekjoon11401: 이항 계수3 (0) | 2021.12.29 |
|---|---|
| Baekjoon11444: 피보나치 수 6 (0) | 2021.12.26 |
| Baekjoon1629: 곱셈 (0) | 2021.12.25 |
| Baekjoon1992: 쿼드트리 (0) | 2021.12.24 |
| Baekjoon1780: 종이의 개수 (0) | 2021.12.23 |