스도쿠 스페셜 저지
| 1 초 | 256 MB | 53530 | 15810 | 9926 | 27.781% |
문제
스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루어진 정사각형 판 위에서 이뤄지는데, 게임 시작 전 일부 칸에는 1부터 9까지의 숫자 중 하나가 쓰여 있다.

나머지 빈 칸을 채우는 방식은 다음과 같다.
- 각각의 가로줄과 세로줄에는 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
- 굵은 선으로 구분되어 있는 3x3 정사각형 안에도 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
위의 예의 경우, 첫째 줄에는 1을 제외한 나머지 2부터 9까지의 숫자들이 이미 나타나 있으므로 첫째 줄 빈칸에는 1이 들어가야 한다.

또한 위쪽 가운데 위치한 3x3 정사각형의 경우에는 3을 제외한 나머지 숫자들이 이미 쓰여있으므로 가운데 빈 칸에는 3이 들어가야 한다.

이와 같이 빈 칸을 차례로 채워 가면 다음과 같은 최종 결과를 얻을 수 있다.

게임 시작 전 스도쿠 판에 쓰여 있는 숫자들의 정보가 주어질 때 모든 빈 칸이 채워진 최종 모습을 출력하는 프로그램을 작성하시오.
입력
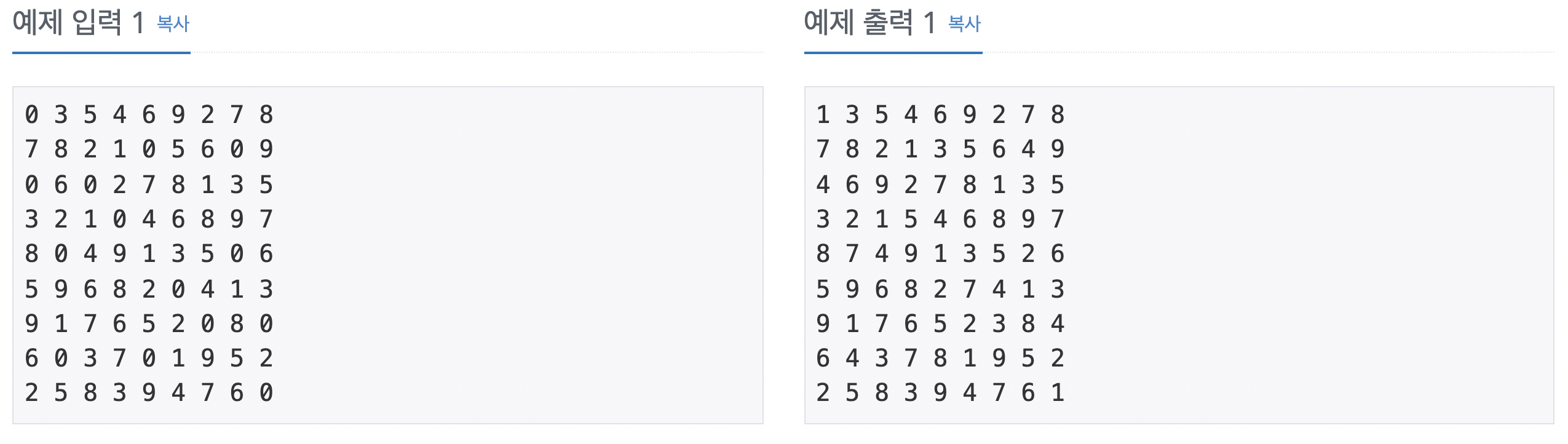
아홉 줄에 걸쳐 한 줄에 9개씩 게임 시작 전 스도쿠판 각 줄에 쓰여 있는 숫자가 한 칸씩 띄워서 차례로 주어진다. 스도쿠 판의 빈 칸의 경우에는 0이 주어진다. 스도쿠 판을 규칙대로 채울 수 없는 경우의 입력은 주어지지 않는다.
출력
모든 빈 칸이 채워진 스도쿠 판의 최종 모습을 아홉 줄에 걸쳐 한 줄에 9개씩 한 칸씩 띄워서 출력한다.
스도쿠 판을 채우는 방법이 여럿인 경우는 그 중 하나만을 출력한다.
제한
- baekjoon의 백트래킹 알고리즘으로 풀 수 있는 입력만 주어진다. 다음은 그 알고리즘의 수행 시간이다.
- C++14: 80ms
- Java: 292ms
- PyPy3: 1172ms
풀이
반례를 조심해야한다. 모든 값이 0으로 이루어진 입력값들이 주어진다. 이 때문에 풀이 방법은 어느 정도 정해져 있는 것 같다.
탐색방법
위의 반례에 의해, 9X9의 2차원 배열 = 최대 81 의 Depth를 가질 수 있는 백트래킹 문제가 되었다.
배열 안에서 0의 값을 찾기 → 그 자리에 1~9 숫자를 대입해 들어갈 수 있는지 체크 → 그 숫자를 대입한 뒤 재귀 호출
위 논리와 더불어 백트래킹에서 가장 중요한 중복 탐색 방지 를 해주어야 한다.
예를 들어 스도쿠 배열 중앙에서 0을 찾았다면 재귀호출할 때 다시 배열의 처음부터 탐색해서 그 다음 0을 찾는 것이 아니라
0을 찾은 위치 그 다음부터 배열을 탐색하는 것이다
현재 탐색하고 있는 행과 열을 곧 Depth 로 나타내면 중복 탐색을 방지할 수 있다.(Depth == 81로도 풀이 가능!)
findAnswer(row, col)현재 메소드의 row, col을 기준으로 스도쿠 배열을 탐색해 0을 찾으면 중복 탐색을 방지할 수 있다
다시 말해 Depth 의 개념을 (row, col)로 나타낸 것이고 col+1 이 곧 Depth +1 과 같은 표현이 된다
row, col 모두 0~8의 값(배열 index)을 가지기 때문에 다음 과정을 추가해준다
col이 9가 되면 다시 0으로 초기화, row는 1 증가
row가 9가 되면 더 이상 탐색할 필요가 없으므로 결과값을 출력
숫자 체크하기
0의 위치에 1~9 숫자를 넣을 수 있는지 판별해주고(if문 + 메소드) 만약 메소드의 값이 참이라면
그 값을 넣은 다음 재귀호출(col + 1)을 한다. 재귀호출 다음에는 다시 바꿔준 값을 0으로 바꿔준다
for(int i=1; i<10; i++) {
if(check(i,row,col)) { // check 메소드를 통해 값이 들어갈 수 있는지 판단
sudoku[row][col]=i; //값을 집어넣고
findAnswer(row,col+1); //재귀호출
sudoku[row][col]=0; //0으로 되돌리기
}
}
3X3 규칙
자기가 속한 3x3 정사각형 안에서도 스도쿠 규칙이 적용되어야 한다.
(row/3)*3, (col/3)*3을 하면 3x3 사각형의 시작점을 구할 수 있다. 시작점을 알고 있으므로
이중 반복문을 이용해 판별해주면 된다.
다른 방법
또는 3x3 사각형이 9개 있다는 것을 이용해 0번~8번 3x3 사각형으로 나눌 수 있다.
(row/3)*3 + col/3 을 하면 현재 (row, col)이 몇 번째 사각형에 있는지 구할 수 있다
코드
import java.util.*;
public class Main {
static int[][] sudoku = new int[9][9]; // 입력값이 들어갈 배열
static StringBuilder sb = new StringBuilder(); // 배열값 출력은 StringBuilder 사용
static boolean found = false; // 첫번째 답안만 출력하기 위해 답을 찾았다고 알려주는 변수 생성
static boolean check(int N, int row, int col) { //N이 그 자리에 들어갈 수 있는지 체크
boolean judge = true; //판별 변수 judge
int row_start = (row/3)*3; // 3x3 사각형 시작점
int col_start = (col/3)*3;
for(int i=0;i<9;i++) { //같은 줄에 있으면 fasle
if(sudoku[row][i]==N || sudoku[i][col]==N) {
judge=false;
i=9;
}
}
for(int i=row_start;i<row_start+3;i++){ //같은 3x3 사각형에 있으면 false
for(int j=col_start; j<col_start+3;j++) {
if(sudoku[i][j]==N) {
judge=false;
}
}
}
return judge;
}
static void findAnswer(int row, int col) {
if(col==9) { //9가 되면 0으로 만들어준다
col=0;
row++;
}
if(row==9) { //row가 9가 되면 출력
found = true;
for(int i=0; i<9;i++) {
for(int j=0;j<9;j++) {
sb.append(sudoku[i][j]+" ");
}
sb.append("\n");
}
System.out.print(sb.toString());
return;
}
if(sudoku[row][col]==0) { //0의 값을 찾으면
for(int i=1; i<10; i++) { // 1~9 대입
if(found)return; //이미 정답을 찾았다면 탐색 중단
if(check(i,row,col)) {
sudoku[row][col]=i;
findAnswer(row,col+1);
sudoku[row][col]=0;
}
}
}else {
findAnswer(row,col+1);
}
return;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
for(int i=0;i<9;i++) {
for(int j=0;j<9;j++) {
sudoku[i][j]=sc.nextInt();
}
}
findAnswer(0,0);
}}
'Study > Baekjoon' 카테고리의 다른 글
| Baekjoon1037: 약수 (0) | 2021.11.29 |
|---|---|
| Baekjoon5086: 배수와 약수 (0) | 2021.11.28 |
| Baekjoon14889: 스타트와 링크 (0) | 2021.11.18 |
| Baekjoon14888: 연산자 끼워넣기 (0) | 2021.11.16 |
| Baekjoon9663: N-Queen (0) | 2021.11.12 |