[Python] Baekjoon10158: 개미
개미
| 0.15 초 (추가 시간 없음) | 256 MB | 10346 | 2845 | 2303 | 33.913% |
문제
가로 길이가 w이고 세로 길이가 h인 2차원 격자 공간이 있다. 이 격자는 아래 그림처럼 왼쪽 아래가 (0,0)이고 오른쪽 위가 (w,h)이다. 이 공간 안의 좌표 (p,q)에 개미 한 마리가 놓여있다. 개미는 오른쪽 위 45도 방향으로 일정한 속력으로 움직이기 시작한다. 처음에 (p,q)에서 출발한 개미는 1시간 후에는 (p+1,q+1)로 옮겨간다. 단, 이 속력으로 움직이다가 경계면에 부딪치면 같은 속력으로 반사되어 움직인다.
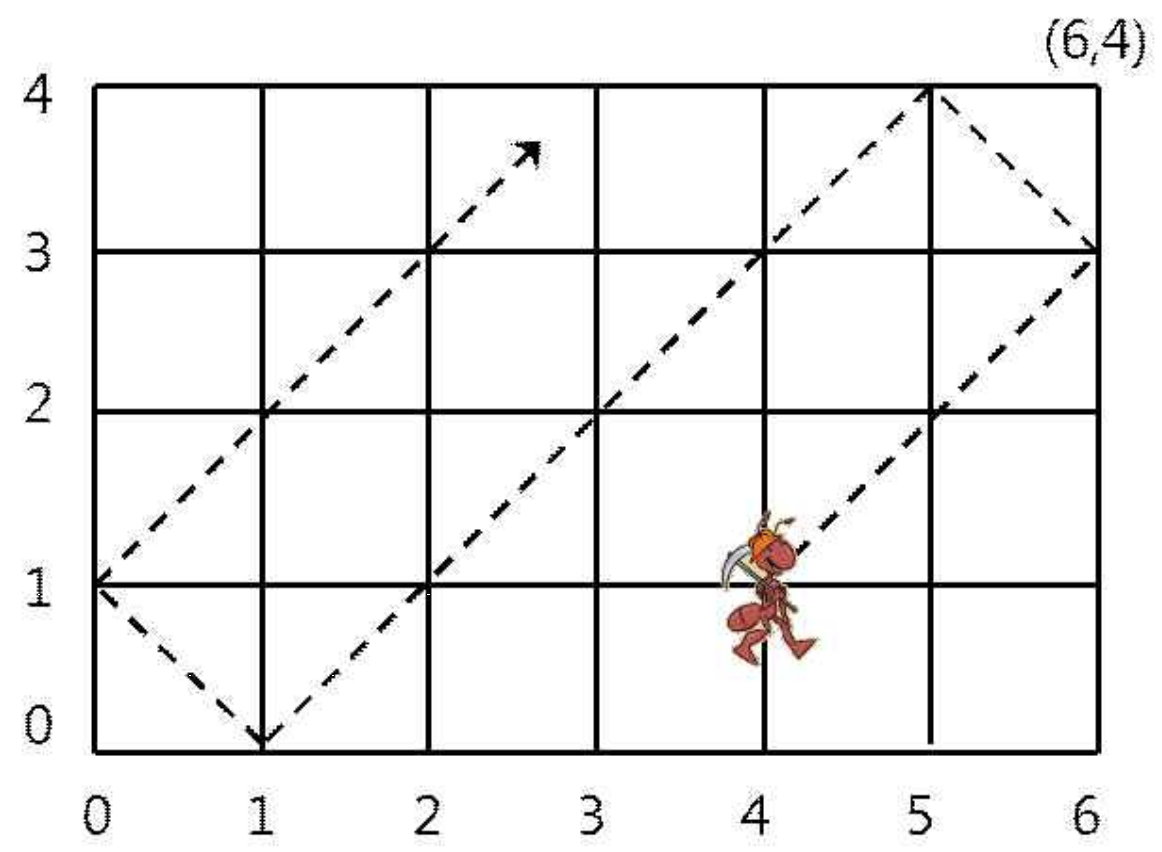
위 그림은 6×4 격자에서 처음에 (4,1)에서 출발한 개미가 움직인 길을 보여주고 있다. 처음에 (4,1)에 있는 개미는 2시간 후에 (6,3)에 있으며 8시간 후에 (0,1)에 있다. 만일 그 개미가 처음에 (5,3)에 있었다면 매 시간마다 (6,4), (5,3), (4,2), (3,1)로 움직인다.
여러분은 크기 w×h인 격자 공간에서 처음에 (p,q)에서 출발하는 개미의 t시간 후의 위치 (x,y)를 계산하여 출력해야 한다. 개미는 절대 지치지 않고 같은 속력으로 이동한다고 가정한다.
문제에서 w와 h는 자연수이며 범위는 2 ≤ w,h ≤ 40,000이다. 그리고 개미의 초기 위치 p와 q도 자연수이며 범위는 각각 0 < p < w과 0 < q < h이다. 그리고 계산할 시간 t의 범위는 1 ≤ t ≤ 200,000,000이다.
입력
첫줄에는 w와 h가 공백을 사이에 두고 주어진다. 그 다음 줄에는 초기 위치의 좌표값 p와 q가 공백을 사이에 두고 주어진다. 3번째 줄에는 개미가 움직일 시간 t가 주어진다.
출력
출력은 t 시간 후에 개미의 위치 좌표 (x,y)의 값 x와 y를 공백을 사이에 두고 출력한다.
풀이
x,y가 동시다발적으로 움직인다고 생각해 처음엔 혼란스러웠는데 좌표를 분리해서 생각해서 풀 수 있었습니다.
x좌표만 생각하면 개미의 위치를 기준으로 오른쪽 왼쪽 진동을 반복합니다.
y좌표도 x좌표처럼 진동합니다.
진동 주기
x의 진동주기를 생각하면 너비 w의 두 배마다 제자리로 돌아오고 방향도 그대로입니다.
즉 2w, 2h는 각각 진동 주기가 됩니다.
시작
시작은 0에서 시작합니다. 원래 개미는 0에 있었지만 p+t, q+t 만큼 움직인것입니다.
진동주기로 나눈 나머지가 곧 실제 움직인 거리
w, h = list(map(int,input().split()))
p, q = list(map(int,input().split()))
t = int(input())
def get(p,t,w):
n = (p+t)%(2*w)
if n<=w:
return n
else:
return 2*w-n
print(get(p,t,w), get(q,t,h))