알고리즘: 그래프(Graph)의 탐색과 메소드 이해&구현
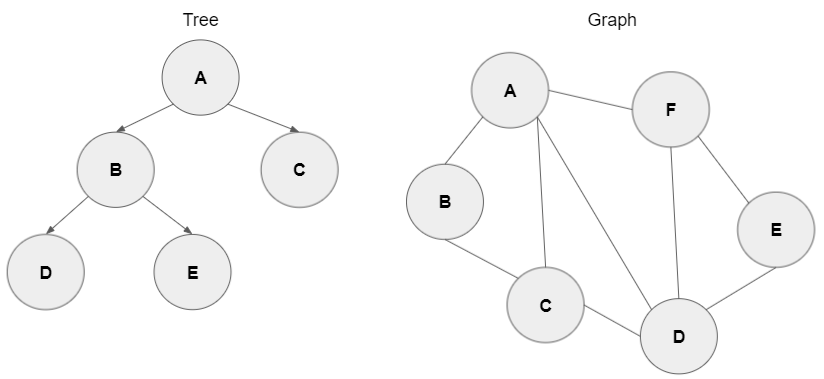
그래프와 트리의 차이
사이클의 유무이다. 노드를 출발해 간선의 방향으로 따라 출발한 노드로 다시 돌아올 수 있다면 사이클이 존재한다고 한다. 하나의 사이클이라도 존재한다면 트리가 될 수 없다. 즉 그래프는 트리를 포함하는 개념이다.
그래프
노드(=정점)와 간선으로 이루어진 자료구조를 뜻한다
구분
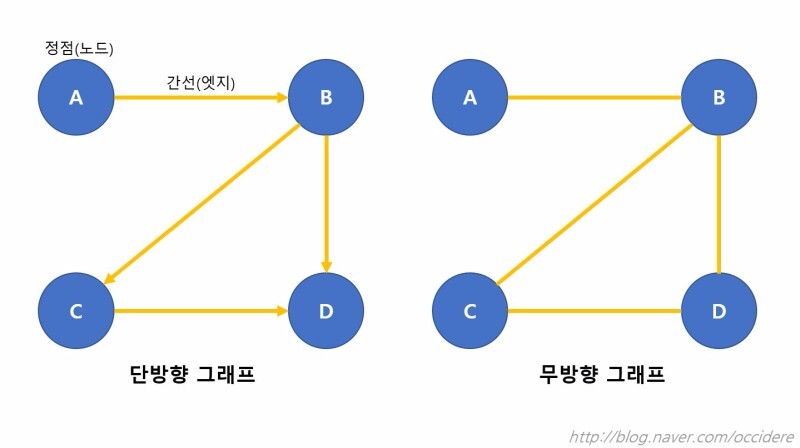
간선에 방향을 표기한 단방향 그래프
연결관계만 표기한 무방향 그래프
행렬화
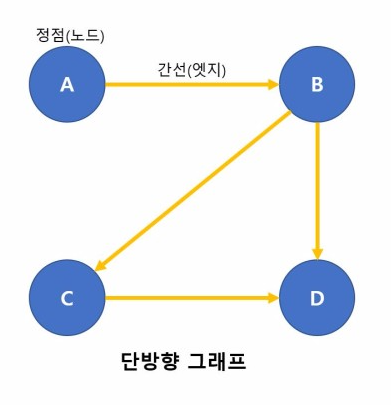
노드와 노드의 연결관계를
행렬로 표현해 연산효율을 높힌다
예시
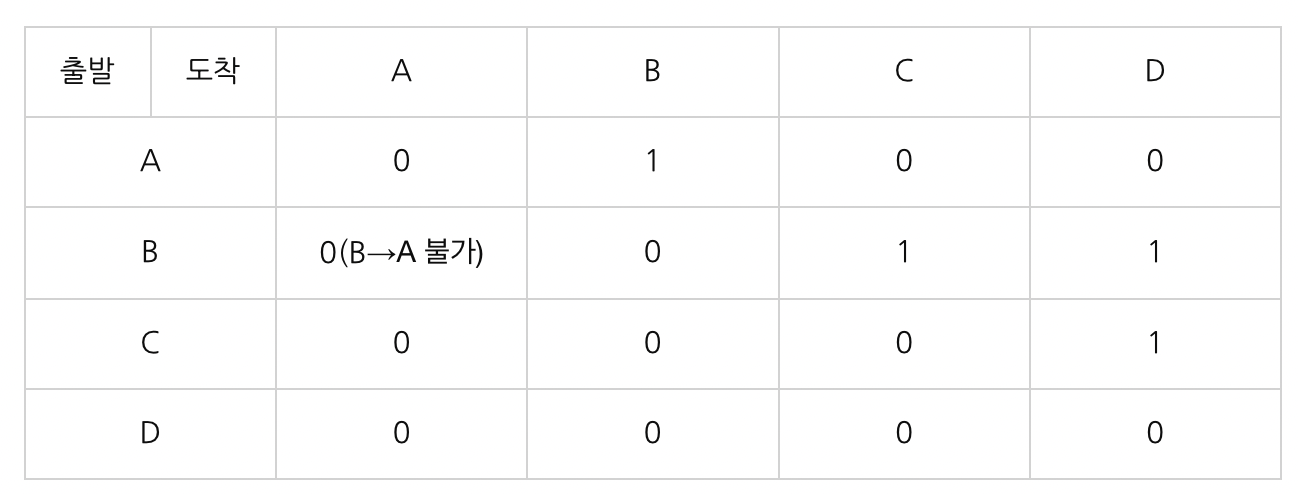
A에서 두 번 움직여서 갈 수 있는 곳은?
= 위 행렬을 제곱한다
위 행렬에서 필요한 정보
1. A에서 갈 수 있는 노드를 구한다

= A에서 갈 수 있는 노드는 B이다
2. 다시 B에서 출발해 도착할 수 있는 곳을 구한다
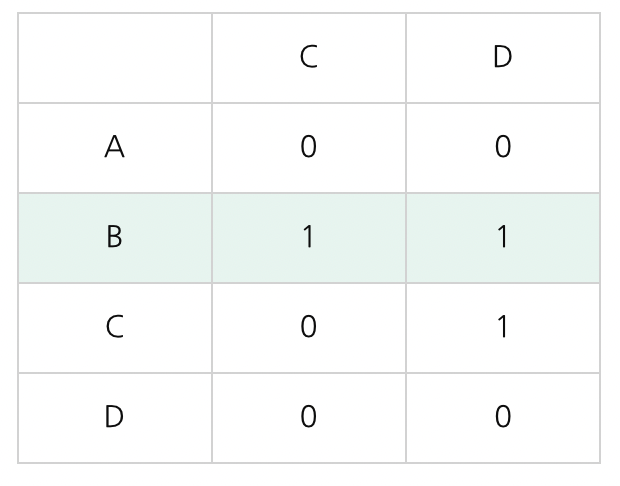
= 총 2 곳
일반화
행렬을 n제곱하면 각 노드에서 출발해
n번 움직여 도착할 수 있는 경우의 수를 구할 수 있다
그래프의 탐색
그래프의 탐색 방식은 2가지가 존재한다
DFS(깊이 우선 탐색) 방식
BFS(너비 우선 탐색) 방식
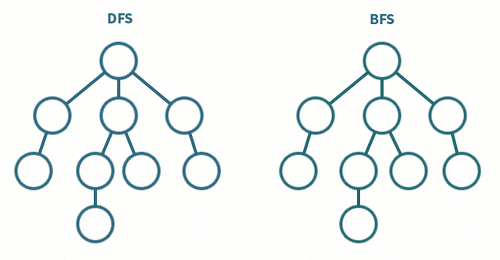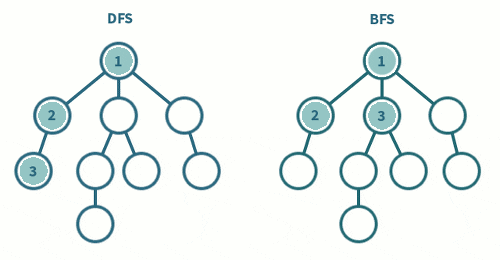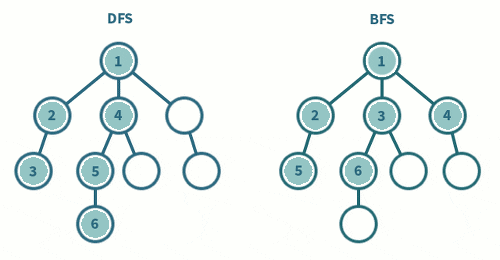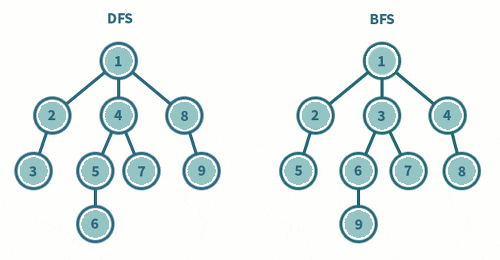
DFS(Depth First Search)
[재귀호출, 스택] 을 통해 구현
하위 노드를 모두 탐색하면
이전 노드로 올라가 재탐색
BFS(Breadth First Search)
[큐]를 통해 구현
현재 탐색하는 인접한 노드를
계속 탐색하는 것을 반복한다
메소드의 구현
백준 1260 문제를 기준으로 구현한다
탐색 시작점은 V로 주어진다고 가정한다
DFS 구현
재귀나 스택을 통해 DFS를 구현한다보통 2차원 배열을 사용해 그래프의 정보를 저장하는데 2차원 배열이 재귀호출과 잘 맞물리므로 재귀호출을 이용해 DFS를 구현해본다.
1) 중복해서 탐색하지 않기 위해 탐색을 했다면 배열을 통해 체크한다.
void dfs(int i){
check[i]=true; //탐색을 시작하면 체크표시
System.out.print(i+" ");
}2) 현재 탐색하는 숫자(i)에 대해서 그 하위 숫자(j)와 연결되어있다면 재귀호출을 통해 방문한다.
for(int j=1;j<=N;j++){
if(arr[i][j]==true && check[j]==false){
//만약 행렬에 연결관계도 존재하고 && 아직 탐색을 하지 않았다면
dfs(j);
}
}3) 위 두 논리를 합쳐 메소드를 만든다.
void dfs(int i){
check[i]=true; //탐색을 시작하면 체크표시
System.out.print(i+" "); //탐색을 완료했으므로 출력
for(int j=1;j<=N;j++){
if(arr[i][j]==true && check[j]==false){
//만약 행렬에 연결관계도 존재하고 && 아직 탐색을 하지 않았다면
dfs(j);
}
}
}
BFS 구현
큐를 통해 BFS를 구현한다. 처음 탐색값 V에 대한 인접한 노드를 큐 입구에 넣어준다. 반복문을 이용하면 1,2,3처럼 오름차순으로 들어갈 것이다. 이 노드들을 출구로 꺼내면 큐 특성상 1,2,3 순서로 다시 나온다. 꺼내면서 해당 노드와 인접한 노드를 입구에 새로 넣어주는 것을 반복하면 BFS를 구현할 수 있다.
1) 큐를 만들어주고 처음 탐색값을 넣는다. DFS처럼 중복해서 탐색하지 않기 위해 배열을 이용해 체크한다.
boolean[] check = new boolean[N+1];
void bfs(){ //처음에 큐를 만들어주기 때문에 매개변수를 사용X
Queue<Integer> queue = new LinkedList<Integer>();
queue.offer(start); //처음값을 넣어준다음
check[start]=true; //체크표시
System.out.print(start+" ");
//처음부: 큐 만들어주고 처음 탐색 값 넣기 & 기록
}2) 큐에 기록된 값이 없을 때까지 반복한다. (isEmpty() 메소드 사용)
3) 현재 탐색하는 노드를 기록해줌과 동시에 삭제한다(poll 메소드 사용)
while(queue.isEmpty()==false){
int now = queue.poll(); //큐 출구의 노드를 빼면서 동시에 기록
for(int i=1;i<=N;i++){
if(arr[now][i] == true && check[i]=false){
//연결관계가 존재하면서 아직 탐색하지 않은 값이면
queue.offer(i); //값을 입구에 넣습니다
check[i]=true;
System.out.print(i+" ");
}
}
}4) 위 논리들을 합친다
public static void bfs() {
Queue<Integer> queue = new LinkedList<Integer>();
queue.offer(V);
check[V]=true;
System.out.print(V+" ");
while(!queue.isEmpty()) {
int now = queue.poll(); //출구의 노드를 빼면서 동시에 저장
for(int i=1;i<=N;i++) {
if(arr[now][i]&&!check[i]) {
queue.offer(i);
check[i]=true;
System.out.print(i+" ");
}
}
}
}